ODE-toolbox¶
Automatic selection and generation of integration schemes for systems of ordinary differential equations
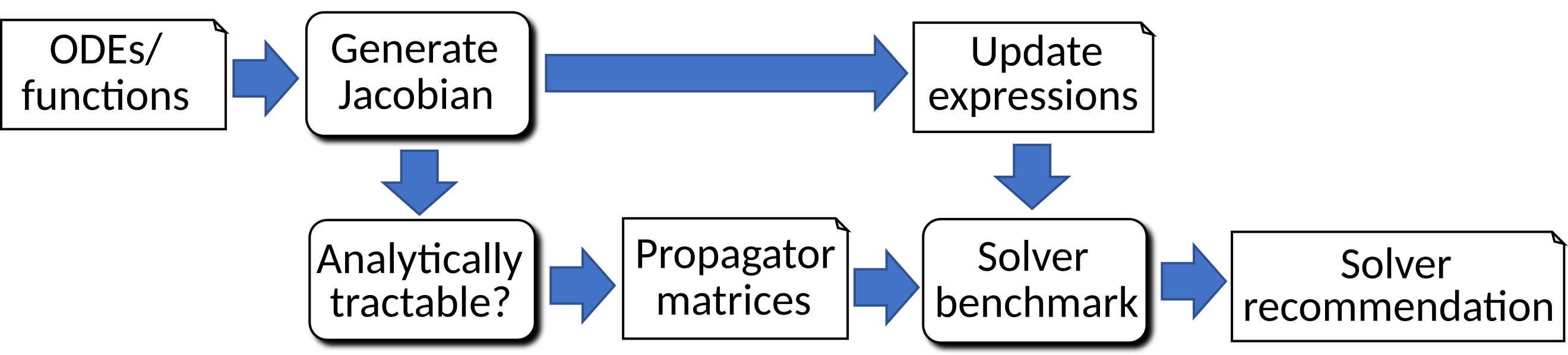
Choosing the optimal solver for systems of ordinary differential equations (ODEs) is a critical step in dynamical systems simulation. ODE-toolbox is a Python package that assists in solver benchmarking, and recommends solvers on the basis of a set of user-configurable heuristics. For all dynamical equations that admit an analytic solution, ODE-toolbox generates propagator matrices that allow the solution to be calculated at machine precision. For all others, first-order update expressions are returned based on the Jacobian matrix.
In addition to continuous dynamics, discrete events can be used to model instantaneous changes in system state, such as a neuronal action potential. These can be generated by the system under test as well as applied as external stimuli, making ODE-toolbox particularly well-suited for applications in computational neuroscience.
ODE-toolbox is intended to be run “off-line”, before commencing the actual simulation. It processes a JSON encoded input of a dynamical system, and produces its output encoded as JSON.
The internal processing carried out by ODE-toolbox can be visually summarised as follows, starting from a system of ODEs and functions of time on the left, and generating propagator matrices, Jacobian (first-order) update expressions, and finally performing solver benchmarking to recommend a particular numerical solver. Each of these steps will be described in depth in the following sections.
ODE-toolbox is written in Python and leverages SymPy for the symbolic manipulation of equations. It was initially developed in the context of the NESTML project, in which the main focus was on the class of spiking neurons presently available in the NEST simulator. It can, however, be used in a standalone fashion, and is broadly applicable to continuous-time dynamical systems as well as systems that undergo instantaneous events (such as neuronal spikes or impulsive forces).
Installation¶
Attention
SymPy releases after 1.4 introduce a fourfold regression in runtime performance on the ODE-toolbox unit tests, compared to SymPy 1.4. Unless this conflicts with other version requirements, we would recommend to use SymPy 1.4 for now (for example, by editing requirements.txt to read sympy==1.4).
Attention
The latest SymPy release at time of writing, 1.10.1, introduces an issue that prevents ODE-toolbox from being used with many common neuron models. Please see https://github.com/sympy/sympy/issues/23417 and use an older SymPy version until this issue has been resolved.
Prerequisites¶
Only Python 3 is supported. ODE-toolbox depends on the Python packages SymPy, Cython, SciPy and NumPy (required), matplotlib and graphviz for visualisation (optional), and pytest for self-tests (also optional). The stiffness tester additionally depends on an installation of PyGSL. If PyGSL is not installed, the test for stiffness is skipped during the analysis of the equations.
All required and optional packages can be installed by running
pip install -r requirements.txt
Installing ODE-toolbox¶
To install, clone the repository, go to the root directory and then run the following command in a terminal:
python setup.py install
If you wish to install into your home directory, add the option --user to the above call.
For further installation hints, please see .travis.yml.
Testing¶
To run the unit and integration tests that come with ODE-toolbox, you can run the following command:
python -m pytest
Please note that this requires the pytest package to be installed.
To increase the verbosity, append the command-line parameters -s -o log_cli=true -o log_cli_level=”DEBUG”.
Usage¶
ODE-toolbox can be used in two ways:
As a command-line application. In this case, the input is stored in a JSON file, and ODE-toolbox is invoked from the command line:
./ode_analyzer.py tests/lorenz_attractor.json
As a Python module:
import odetoolbox, json indict = json.load(open("tests/lorenz_attractor.json")) odetoolbox.analysis(indict)
See the tests (e.g. test_lorenz_attractor.py) for more examples.
The JSON file and Python dictionary are completely equivalent in content and form, described in the Input section below.
Several boolean flags can additionally be passed. When ODE-toolbox is used via its API, these exist as function parameters, for example:
odetoolbox.analysis(indict, disable_stiffness_check=True)
If the command line is used, they can be passed as arguments:
./ode-analyzer.py tests/lorenz_attractor.json --disable-stiffness-check
The following flags exist:
| Name | Default | Description |
|---|---|---|
disable_analytic_solver |
False | Set to True to return numerical solver recommendations, and no propagators, even for ODEs that are analytically tractable. |
disable_stiffness_check |
False | Set to True to disable stiffness check. |
preserve_expressions |
False | Set to True, or a list of strings corresponding to individual variable names, to disable internal rewriting of expressions, and return same output as input expression where possible. Only applies to variables specified as first-order differential equations. |
log_level |
logging.WARN |
Sets the logging threshold. Logging messages which are less severe than log_level will be ignored. Log levels can be provided as an integer or string, for example “INFO” (more messages) or “WARN” (fewer messages). For a list of valid logging levels, see https://docs.python.org/3/library/logging.html#logging-levels |
Input¶
The JSON input dictionary that is passed to ODE-toolbox contains dynamics, numerical parameters, and global options. Documentation may optionally be provided as a string.
All expressions are parsed as SymPy expressions, and subsequently simplified through sympy.simplify(). There are several predefined symbols, such as e and E for Euler’s number, trigonometric functions, etc. t is assumed to represent time. The list of predefined symbols is defined in shapes.py, as the static member Shape._sympy_globals. Variable names should be chosen such that they do not conflict with the predefined symbols.
Dynamics¶
All dynamical variables have a variable name, a differential order, and a defining expression. The overall dynamics is given as a list of these definitions. For example, we can define an alpha shape kernel \(g\) with time constant \(\tau\) as follows:
This can be entered as:
"dynamics":
[
{
"expression": "g'' = -1 / tau**2 * g - 2/tau * g'"
}
]
Instead of a second-order differential equation, we can equivalently describe the kernel shape as a function of time:
This can be entered as:
"dynamics":
[
{
"expression": "g = (e / tau) * t * exp(-t / tau)"
}
]
Expressions can refer to variables defined in other expressions. For example, a third, equivalent formulation of the alpha shape is as the following system of two coupled first-order equations:
This can be entered as:
"dynamics":
[
{
"expression": "g' = h",
},
{
"expression": "h' = -g / tau**2 - 2 * h / tau",
}
]
Initial values¶
As many initial values have to be specified as the differential order requires, that is, none for functions of time, one for a one-dimensional system of ODEs, and so on. Continuing the second-order alpha function example:
"dynamics":
[
{
"expression": "g'' = -1 / tau**2 * g - 2/tau * g'"
"initial_values":
{
"g" : "0",
"g'" : "e / tau"
}
}
]
If only one initial value is required, the following simpler syntax may be used, which omits the variable name:
"dynamics":
[
{
"expression": "g' = -g / tau"
"initial_value": "e / tau"
}
]
Upper and lower thresholds¶
Neuronal dynamics is typically characterised by a discontinuous jump upon action potential firing. To model this behaviour, an upper and lower bound can be defined for each input variable. When either bound is reached, the state of that variable is reset to its initial value.
Thresholds are mainly of interest when doing stiffness testing, and only apply to equations that are solved by the numerical integrator. Testing for threshold crossing and reset of the state variable(s) occurs at the beginning of every timestep.
"dynamics":
[
{
"expression": "V_m' = (-g_L * (V_m - E_L) - g_ex * (V_m - E_ex)) / C_m
"initial_value": "-70",
"upper_bound": "-55"
}
}
Parameters¶
It is not necessary to supply any numerical values for parameters. The expressions are analysed symbolically, and in some cases a set of symbolic propagators will be generated. However, in some cases (in particular when doing stiffness testing), it can be important to simulate with a particular set of parameter values. In this case, they can be specified in the global parameters dictionary. This dictionary maps parameter names to default values, for example:
"parameters":
{
"N": "10",
"C_m": "400.",
"tau": "1 - 1/e",
"I_ext": "30E-3"
}
Spiking stimulus for stiffness testing¶
Spike times for each variable can be read directly from the JSON input as a list, or be generated according to a constant frequency or Poisson distribution. The general format is as follows: any number of stimuli can be defined in the global list “stimuli”. Each entry in the list is a dictionary containing parameters, and a “variables” attribute that specifies which dynamical variables are affected by this particular spike generator. For example:
"stimuli":
[
{
"type": "poisson_generator",
"rate": "10.",
"variables": ["g_in'", "g_ex'"]
}
]
The type is one of “poisson_generator”, “regular” or “list”. The Poisson and regular spiking generators only have one parameter: rate. When the selected type is “list”, a list of predefined spike times can be directly supplied under the key “list”, separated by spaces, as such:
{
"type": "list",
"list": "5E-3 10E-3 20E-3 15E-3 50E-3",
"variables": ["I'"]
}
Note that the amplitude of a spike response is a result of the magnitude of its initial values.
Global options¶
Further options for the integrator, decision criteria for solver selection and so on, can be specified in the global options dictionary, for example:
"options" : {
"sim_time": "100E-3",
"max_step_size": ".25E-3"
}
The following global options are defined. Note that all are typically formatted as strings when encoding into JSON.
| Name | Default | Type | Description |
|---|---|---|---|
integration_accuracy_abs |
1E-9 | float | Absolute error bound for all numerical integrators that are used. |
integration_accuracy_rel |
1E-9 | float | Relative error bound for all numerical integrators that are used. |
output_timestep_symbol |
"__h" |
string | Generated propagators are a function of the simulation timestep. This parameter gives the name of the variable that contains the numerical value of the timestep during simulation. |
sim_time |
100E-3 | float | Total simulated time. |
max_step_size |
999 | float | Maximum step size during simulation (e.g. for stiffness testing solvers). |
differential_order_symbol |
“__d” |
string | String appended n times to output variable names to indicate differential order n. |
simplify_expression |
“sympy.simplify(expr)” |
string | For all expressions expr that are rewritten internally: the contents of this parameter string are evaluated with eval() in Python to obtain the final output expression. Override for custom expression simplification steps. Example: "sympy.logcombine(sympy.powsimp(sympy.expand(expr)))". |
Output¶
The analysis output is returned in the form of a Python dictionary, or an equivalent JSON file.
During analysis, ODE-toolbox rewrites the differential notation from single quotation marks into characters that are typically compatible with variable names; by default every quotation mark is rewritten into the string specified as the global parameter differential_order_symbol (by default, “__d”).
ODE-toolbox will return a list of solvers. Each solver has the following keys:
“solver”: a string containing the solver recommendation. Starts with either“analytical”or“numeric”.“state_variables”: an unordered list containing all variable symbols.“initial_values”: a dictionary that maps each variable symbol (in string form) to a SymPy expression. For example“g” : “e / tau”.“parameters”: only present when parameters were supplied in the input. The input parameters are copied into the output for convenience.
Analytic solvers have the following extra entries:
“update_expressions”: a dictionary that maps each variable symbol (in string form) to a SymPy propagator expression. The interpretation of an entry“g” : “g * __P__g__g + h * __P__g__h”is that, at each integration timestep, when the state of the system needs to be updated from the current time \(t\) to the next step \(t + \Delta t\), we assign the new value“g * __P__g__g + h * __P__g__h”to the variableg. Note that the expression is always evaluated at the old time \(t\); this means that when more than one state variable needs to be updated, all of the expressions have to be calculated before updating any of the variables.propagators: a dictionary that maps each propagator matrix entry to its defining expression; for example“__P__g__h” : “__h*exp(-__h/tau)”
Numeric solvers have the following extra entries:
“update_expressions”: a dictionary that maps each variable symbol (in string form) to a SymPy expression that is its Jacobian, that is, for a symbol \(x\), the expression is equal to \(\frac{\delta x}{\delta t}\).
Analytic solver generation¶
If an ODE is constant-coefficient and linear, an analytic solution can be computed. Analytically solvable ODEs can also contain dependencies on other analytically solvable ODEs, but an otherwise analytically tractable ODE cannot depend on an ODE that can only be solved numerically. In the latter case, no analytic solution will be computed.
For example, consider an integrate-and-fire neuron with two alpha-shaped kernels (I_shape_in and I_shape_gap), and one nonlinear kernel (I_shape_ex). Each of these kernels can be expressed as a system of ODEs containing two variables. I_shape_in is specified as a second-order equation, whereas I_shape_gap is explicitly given as a system of two coupled first-order equations, i.e. as two separate dynamics entries with names I_shape_gap1 and I_shape_gap2. Both formulations are mathematically equivalent, and ODE-toolbox treats them the same following input processing. The membrane potential V_rel is expressed relative to zero, making it a homogeneous equation and one that could be analytically solved, if it were not for its dedependence on the quantity I_shape_ex which itself requires a numeric solver due to its nonlinear dynamics.
During processing, a dependency graph is generated, where each node corresponds to one dynamical variable, and an arrow from node a to b indicates that a depends on the value of b. Boxes enclosing nodes mark input shapes that were specified as either a direct function of time or a higher-order differential equation, and were expanded to a system of first-order ODEs.
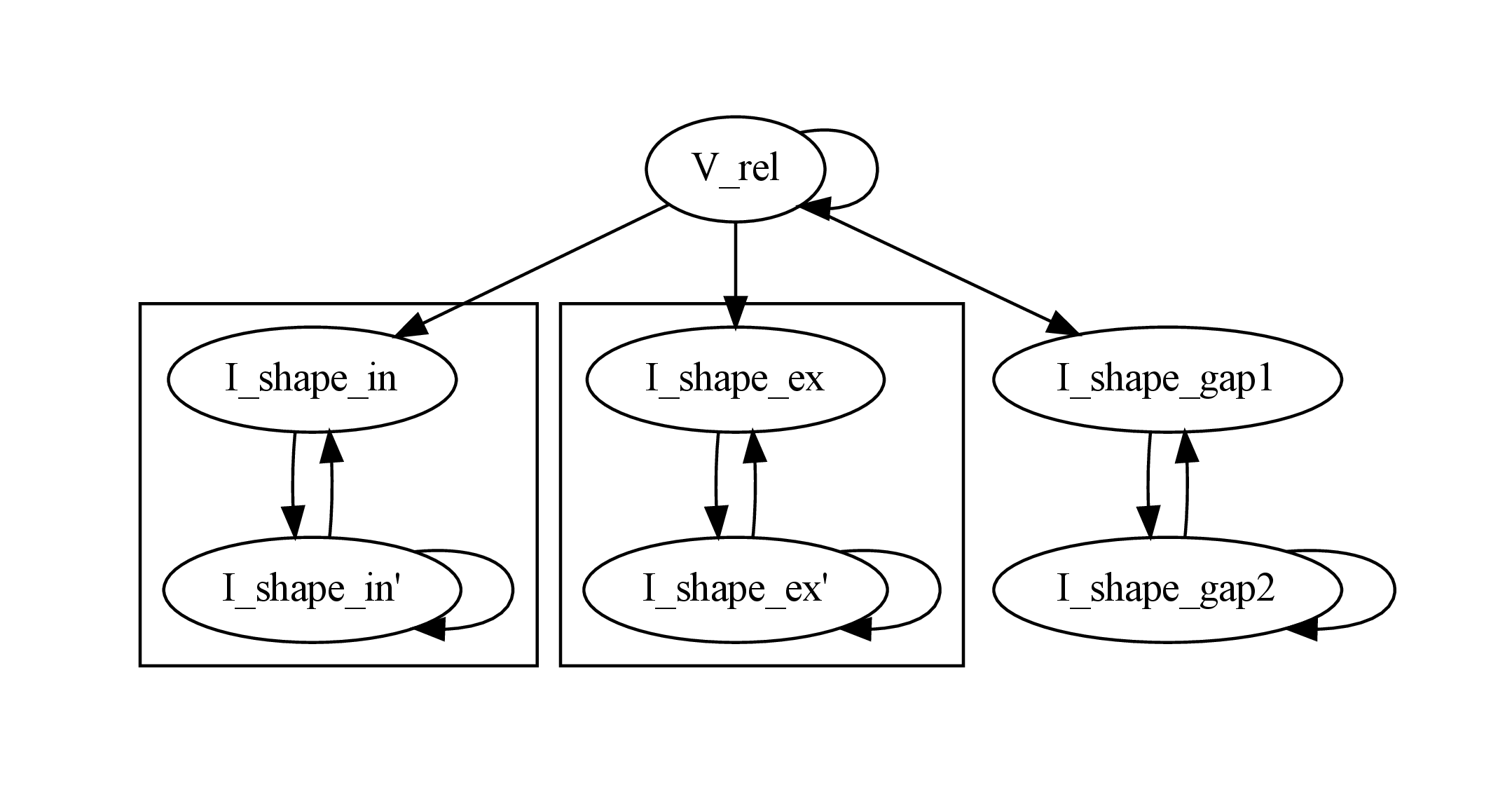
Each variable is subsequently marked according to whether it can, by itself, be analytically solved. This is indicated by a green colour.
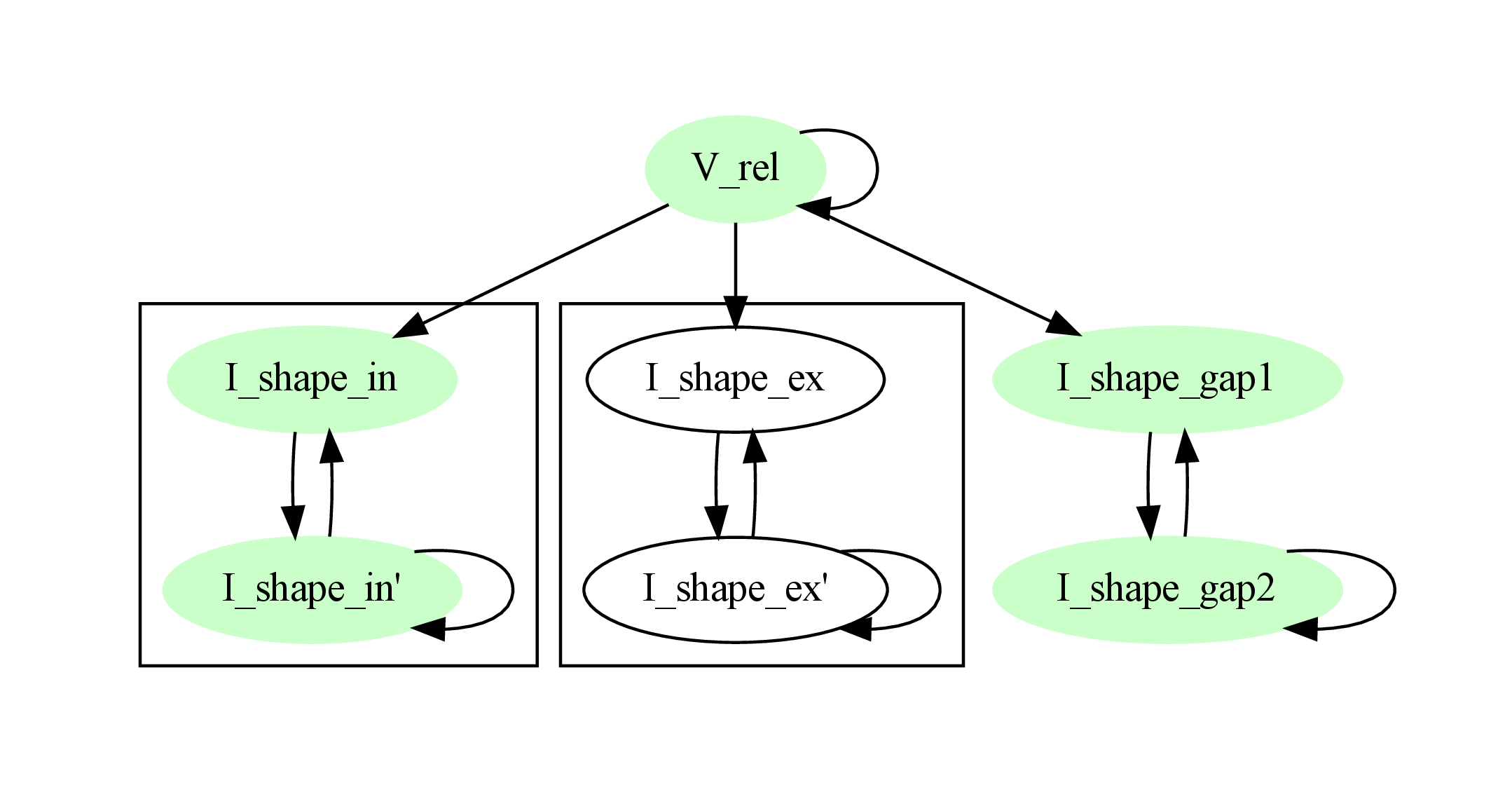
In the next step, variables are unmarked as analytically solvable if they depend on other variables that are themselves not analytically solvable. In this example, V_rel is unmarked as it depends on the nonlinear excitatory kernel.
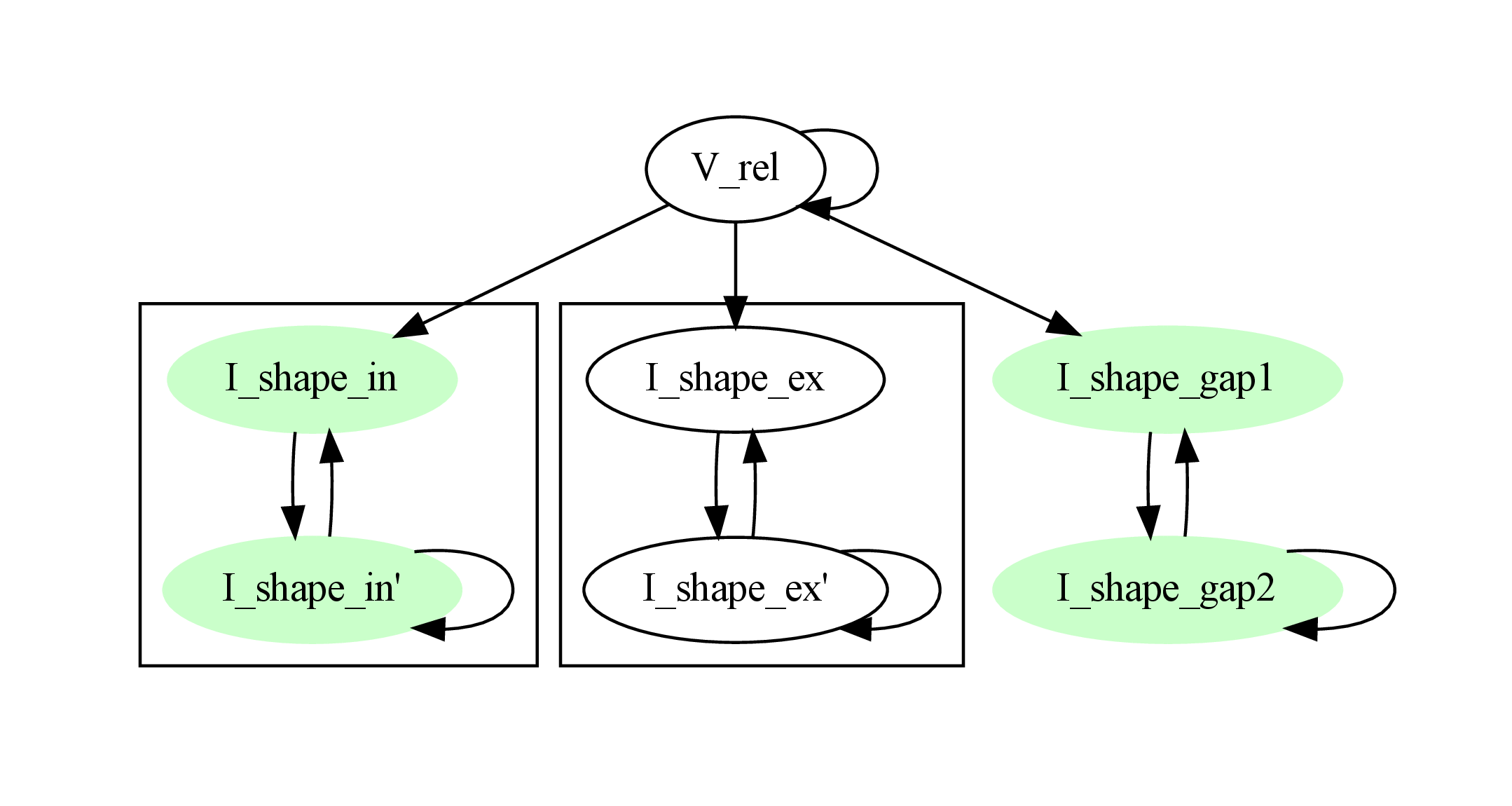
The analytic solution for all green nodes is computed in the form of a propagator matrix. See the section Computing the propagator matrix for more details.
Numeric solver selection criteria¶
Numeric solvers are automatically benchmarked on solving the provided system of ODEs, at a certain requested tolerance. Selecting the optimal solver is based on a set of rules, defined in StiffnessTester.draw_decision(). The logic is as follows.
Let the machine precision (defined as the smallest representable difference between any two floating-point numbers) be written as \(\varepsilon\).
Then the minimum permissible timestep is defined as \(\varepsilon\,\cdot\)machine_precision_dist_ratio.
- If the minimum step size recommended by all solvers is smaller than the minimum permissible timestep, a warning is issued.
- If the minimum step size for the implicit solver is smaller than the minimum permissible timestep, recommend the explicit solver.
- If the minimum step size for the explicit solver is smaller than the minimum permissible timestep, recommend the implicit solver.
- If the average step size for the implicit solver is at least
avg_step_size_ratiotimes as large as the average step size for the explicit solver, recommend the implicit solver. - Otherwise, recommend the explicit solver.
| Name | Default | Description |
|---|---|---|
avg_step_size_ratio |
6 | Ratio between average step sizes of implicit and explicit solver. Larger means that the explicit solver is more likely to be selected. |
machine_precision_dist_ratio |
10 | Disqualify a solver if its minimum step size comes closer than this ratio to the machine precision. |
Internal representation¶
For users who want to modify/extend ODE-toolbox.
Initially, individual expressions are read from JSON into Shape instances. Subsequently, all shapes are combined into a odetoolbox.system_of_shapes.SystemOfShapes instance, which summarises all provided dynamical equations in the canonical form \(\mathbf{x}' = \mathbf{Ax} + \mathbf{b} + \mathbf{c}\), with matrix \(\mathbf{A}\) containing the linear part of the system dynamics, vector \(\mathbf{b}\) containing only real numbers and constant parameters, and vector \(\mathbf{c}\) containing nonlinear terms.
Converting direct functions of time¶
The aim is to find a representation of the form \(a_0 f + a_1 f' + ... + a_{n-1} f^{(n-1)} = f^{(n)}\), with \(a_i\in\mathbb{R}\,\forall 0 \leq i < n\). The approach taken here [5] works by evaluating the function \(f(t)\) at times \(t = t_0, t_1, \ldots t_n\), which results in \(n\) equations, that we can use to solve for the coefficients of the potentially \(n\)-dimensional dynamical system.
- Begin by assuming that the dynamical system is of order \(n\).
- Find timepoints \(t = t_0, t_1, ..., t_n\) such that \(f(t_i) \neq 0 \forall 0 \leq i \leq n\). The times can be selected at random.
- Formulate the equations as \(\mathbf{X} \cdot \left[\begin{matrix}a_0\\a_1\\\vdots\\a_{n-1}\end{matrix}\right] = \left[\begin{matrix}f^{(n)}(t_0)\\f^{(n)}(t_1)\\\vdots\\f^{(n)}(t_n)\end{matrix}\right]\) with \(\mathbf{X} = \left[\begin{matrix} f(t_0) & \cdots & f^{(n-1)}(t_0) \\ f(t_1) & \cdots & f^{(n-1)}(t_1) \\ \vdots & & \vdots \\ f(t_n) & \cdots & f^{(n-1)}(t_n) \end{matrix}\right]\).
- If \(\mathbf{X}\) is invertible, the equation can be solved for \(a_0\ldots a_{n-1}\).
- If \(\mathbf{X}\) is not invertible, increase \(n\) (up to some predefined maximum order \(n_{max}\)). If \(n_{max}\) is reached, fail.
This algorithm is implemented in odetoolbox.shapes.Shape.from_function().
Computing the propagator matrix¶
The propagator matrix \(\mathbf{P}\) is derived from the system matrix by matrix exponentiation:
If the imaginary unit \(i\) is found in any of the entries in \(\mathbf{P}\), fail. This usually indicates an unstable (diverging) dynamical system. Double-check the dynamical equations.
In some cases, elements of \(\mathbf{P}\) may contain fractions that have a factor of the form param1 - param2 in their denominator. If at a later stage, the numerical value of param1 is chosen equal to that of param2, a numerical singularity (division by zero) occurs. To avoid this issue, it is necessary to eliminate either param1 or param2 in the input, before the propagator matrix is generated. ODE-toolbox will detect conditions (in this example, param1 = param2) under which these singularities can occur. If any conditions were found, log warning messages will be emitted during the computation of the propagator matrix. A condition is only reported if the system matrix \(A\) is defined under that condition, ensuring that only those conditions are returned that are purely an artifact of the propagator computation.
Computing the update expressions¶
The update expressions formulate the way in which the propagators are used to compute the new state from the current state. For instance, for a simple leaky integrate-and-fire neuron with membrane potential \(V_m\) and a decaying exponential-shaped synaptic kernel \(I_{syn}\), the update expressions are of the form:
In the case of an autonomous ODE (for which \(\textbf{b}\) contains a nonzero, constant entry, and the corresponding entry in \(\textbf{A}\) is zero), the update equation is of the form:
For example for the ODE:
the update equation is:
In the case of an inhomogenous ODE (for which \(\textbf{b}\) contains a nonzero, constant entry, but the corresponding entry in \(\textbf{A}\) is nonzero), the update equation is of the form:
For example for the ODE:
the update equation is:
Working with large expressions¶
In several places during processing, a SymPy expression simplification (simplify()) needs to be performed to ensure correctness. For very large expressions, this can result in long wait times, while it is most often found that the resulting system of equations has no analytical solution anyway. To address these performance issues with SymPy, we introduce the expression_simplification_threshold constant, which causes expressions whose string representation is longer than this number of characters to be skipped when simplifying expressions. The default value is 1000.
Examples¶
Several example input files can be found under tests/*.json. Some highlights:
- Lorenz attractor
- Morris-Lecar neuron model
- Integrate-and-fire neuron with alpha-kernel postsynaptic currents, including Poisson spike generator for stiffness test
- Integrate-and-fire neuron with alpha-kernel postsynaptic conductances
- Canonical, two-dimensional stiff system Example 11.57 from Dahmen, W., and Reusken, A. (2005). Numerik fuer Naturwissenschaftler. Berlin: Springer
Stiffness testing¶
This example correponds to the unit test in test_stiffness.py, which simulates the Morris-Lecar neuron model in morris_lecar.json. The plot shows the two state variables of the model, V and W, while in the lower panel the solver timestep recommendation is plotted at each step. This recommendation is returned by each GSL solver. Note that the avg_step_size_ratio selection criterion parameter refers to the average of this value across the entire simulation period.
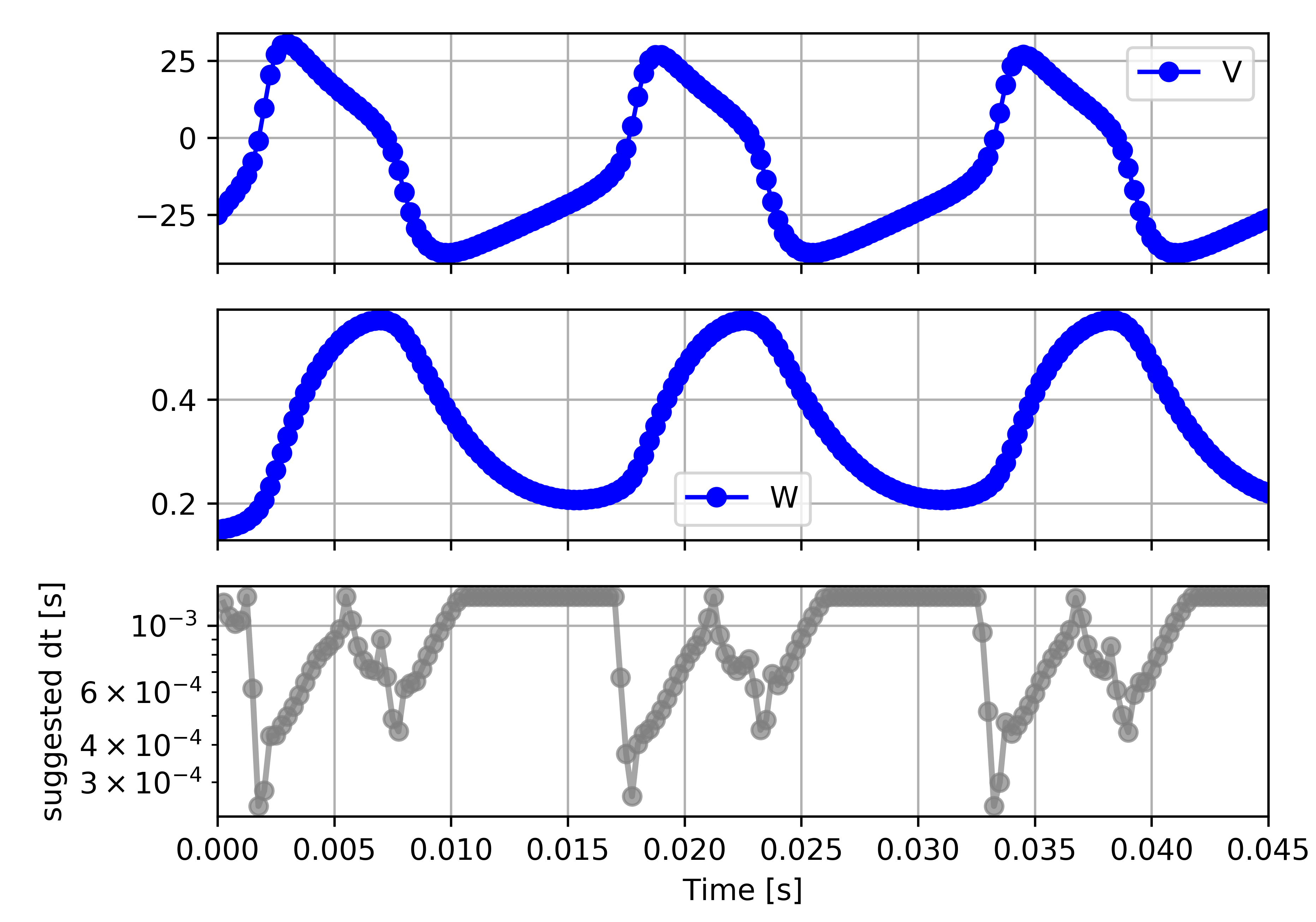
test_stiffness.py tests that for a tighter integration accuracy, the solver recommendation for this example changes from “explicit” (non-stiff) to “implicit” (stiff).
From ODE-toolbox results dictionary to simulation¶
ODE-toolbox provides two classes that can perform numerical simulation on the basis of the results dictionary returned by ODE-toolbox: AnalyticIntegrator, which simulates on the basis of propagators and returns precise values, and MixedIntegrator, which in addition performs numerical integration using GSL (for example, using pygsl.odeiv.step_rk4 or pygsl.odeiv.step_bsimp). These integrators both use sympy.parsing.sympy_parser to parse the expression strings from the ODE-toolbox results dictionary, and then use the SymPy expression evalf() method to evaluate to a floating-point value.
The file test_analytic_solver_integration.py contains an integration test that uses AnalyticIntegrator and the propagators returned from ODE-toolbox to simulate a simple dynamical system; in this case, an integrate-and-fire neuron with alpha-shaped postsynaptic currents. It compares the obtained result to a handwritten solution, which is simulated analytically and numerically independent of ODE-toolbox. The following results figure shows perfect agreement between the three simulation methods:
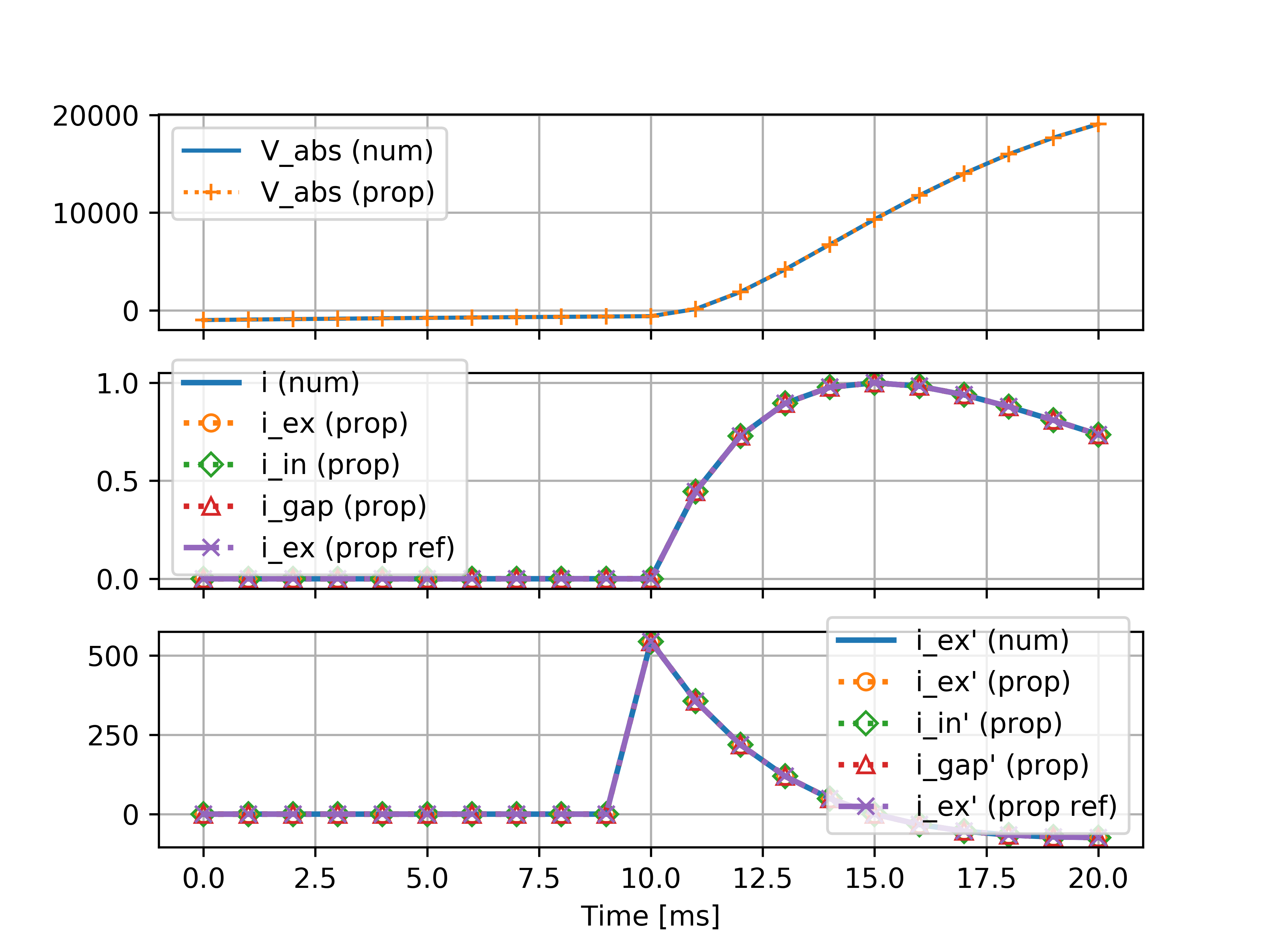
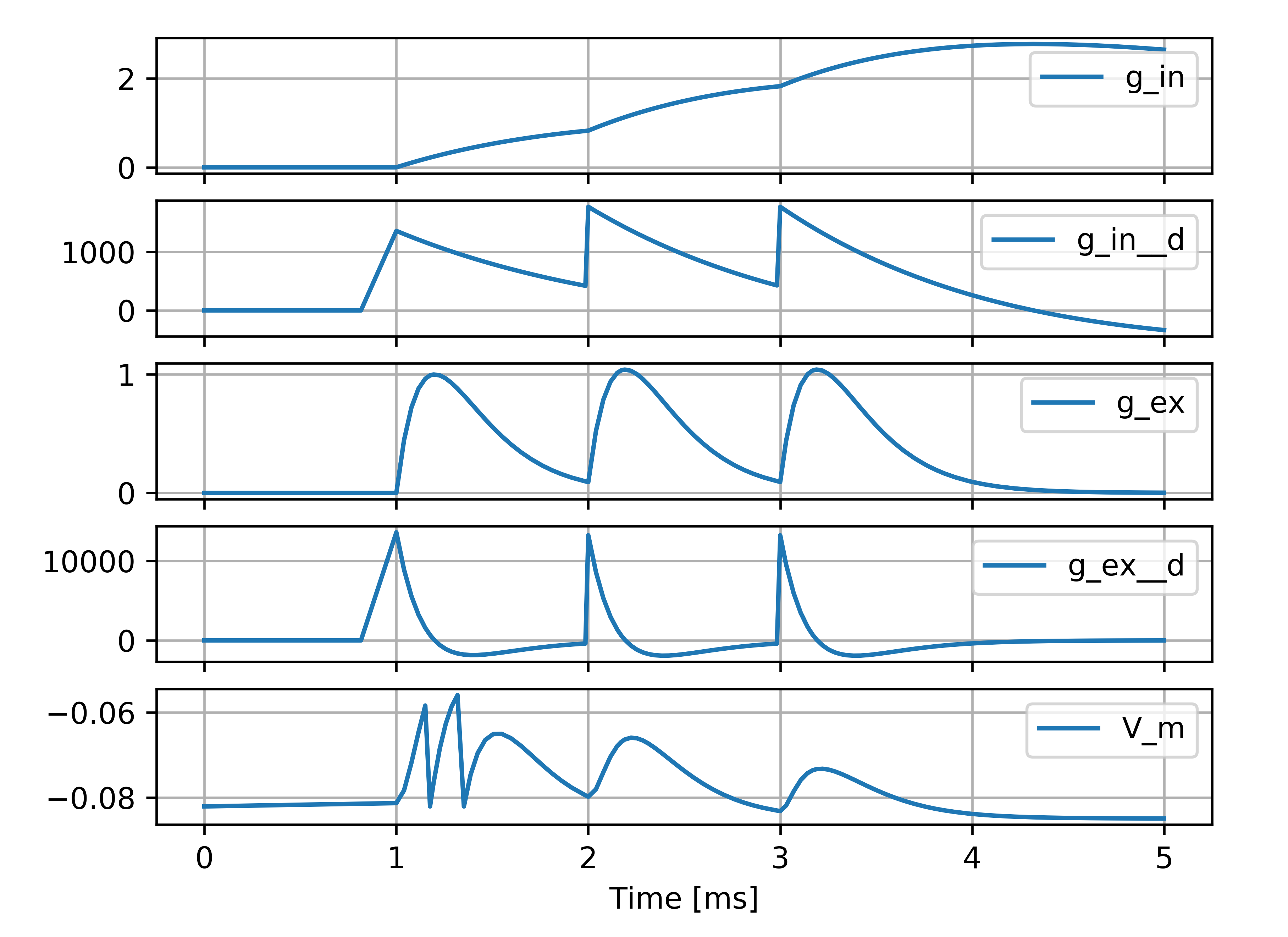
The file test_mixed_integrator_numeric.py contains an integration test, that uses MixedIntegrator and the results dictionary from ODE-toolbox to simulate the same integrate-and-fire neuron with alpha-shaped postsynaptic response, but purely numerically (without the use of propagators). In contrast to the AnalyticIntegrator, enforcement of upper- and lower bounds is supported, as can be seen in the behaviour of \(V_m\) in the plot that is generated:
Caching of results¶
TODO
Not implemented yet.
Some operations on SymPy expressions can be quite slow (see the section Working with large expressions).
Even dynamical systems of moderate size can require a few minutes of processing time, in large part due to SymPy calls, and solver selection.
To speed up processing, a caching mechanism analyses the final system matrix \(\mathbf{A}\) and rewrites it as a block-diagonal matrix \(\mathbf{A} = \text{diag}(\mathbf{B}_1, \mathbf{B}_2, \dots, \mathbf{B}_k)\), where each of \(\mathbf{B}_1, \mathbf{B}_2, \dots, \mathbf{B}_k\) is square.
For propagators, we note that
API documentation¶
The documentation of all Python classes and functions in the odetoolbox package can be found here:
Contributions and getting help¶
The primary development of ODE-toolbox happens on GitHub, at https://github.com/nest/ode-toolbox. If you encounter any issue, please create an new entry in the GitHub issue tracker. Pull requests are welcome.
Citing ODE-toolbox¶
If you use ODE-toolbox in your work, please cite it depending on the version you are using. (It is recommended to use the latest release version whenever possible.)
For version 2.5:
| [1] | Charl Linssen, Shraddha Jain, Pooja N. Babu, Abigail Morrison and Jochen M. Eppler (2022) ODE-toolbox: Automatic selection and generation of integration schemes for systems of ordinary differential equations. Zenodo. doi:10.5281/zenodo.7193351. |
For version 2.4:
| [2] | Charl Linssen, Pooja N. Babu, Abigail Morrison and Jochen M. Eppler (2021) ODE-toolbox: Automatic selection and generation of integration schemes for systems of ordinary differential equations. Zenodo. doi:10.5281/zenodo.5768597. |
For versions 2.3, 2.2 and 2.1:
| [3] | Charl Linssen, Shraddha Jain, Abigail Morrison and Jochen M. Eppler (2020) ODE-toolbox: Automatic selection and generation of integration schemes for systems of ordinary differential equations. Zenodo. doi:10.5281/zenodo.4245012. |
For version 2.0:
| [4] | Charl Linssen, Abigail Morrison and Jochen M. Eppler (2020) ODE-toolbox: Automatic selection and generation of integration schemes for systems of ordinary differential equations. Zenodo. doi:10.5281/zenodo.3822082. |
References¶
| [5] | Inga Blundell, Dimitri Plotnikov, Jochen Martin Eppler and Abigail Morrison (2018) Automatically selecting a suitable integration scheme for systems of differential equations in neuron models. Front. Neuroinform. doi:10.3389/fninf.2018.00050. |
Acknowledgements¶
Logo design by Konstantin Perun.
This software was initially supported by the JARA-HPC Seed Fund NESTML - A modeling language for spiking neuron and synapse models for NEST and the Initiative and Networking Fund of the Helmholtz Association and the Helmholtz Portfolio Theme Simulation and Modeling for the Human Brain.
This software was developed in part or in whole in the Human Brain Project, funded from the European Union’s Horizon 2020 Framework Programme for Research and Innovation under Specific Grant Agreements No. 720270, 785907 and 945539 (Human Brain Project SGA1, SGA2 and SGA3, respectively).
License¶
Copyright (C) 2017 The NEST Initiative
ODE-toolbox is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 2 of the License, or (at your option) any later version.
ODE-toolbox is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.
You should have received a copy of the GNU General Public License along with ODE-toolbox. If not, see http://www.gnu.org/licenses/.